Vertex Displacement

Sections :

• Shader Stages
• Vertex Displacement
• Recalculating Normals (Added 31 Jan 2023)
  • Per-Fragment
  • Per-Vertex
• Bounds
• Uses
• Examples
  • Swaying Grass
  • Swimming Motion (Fish)
  • Wings Motion (Butterfly, or Bird)
  • Other (links to tutorials)

Shader Stages

Shaders contain multiple shader programs or stages. At the very least, a shader will contain a Vertex and Fragment stage. The fragment stage is responsible for colour/shading using interpolated data from the vertex stage. The vertex stage is responsible from passing data from the mesh, such as vertex positions - manipulating these is the focus of this post. My Intro To Shaders post goes through these stages in a bit more detail.

Unity also has Surface Shaders, which generates these vertex/fragment stages behind the scenes. But this is only available in the Built-in RP currently. If you’re using one of these, there is a vertex modification function that you can add using vertex:FunctionName to the surface pragma (there are some examples on this Surface Shader Examples page in the docs).

In Shader Graph, nodes that are connected to the Master node’s Vertex ports are written to this vertex shader stage. In newer versions the Master Stack separates the Vertex and Fragment stages into separate areas to make it clear which ports fit into which stage. There is also now an option to create Custom Interpolators to force calculations to be handled in the vertex stage, which can then be passed through to the fragment.

When attempting to connect a node between the vertex and fragment stages, they sometimes may not connect. It is usually a good idea to keep the two parts as separate as possible. Note that there are also certain nodes that won’t work in the Vertex stage, so won’t connect. This is most common when using the Sample Texture 2D node. If you need to sample a texture in the vertex stage you must use the Sample Texture 2D LOD node instead! Can see more examples of Fragment-Only nodes here.

Vertex Displacement

The Vertex Position port on the Master node/stack requires the position to be defined in Object space as it will handle conversions to other spaces automatically. Sometimes using other spaces is necessary in calculations, but the final position would need to be transformed to Object, which could be done using a Transform node.

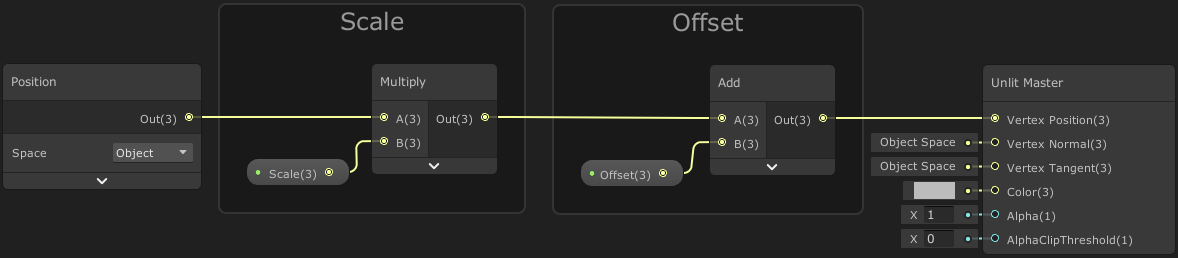
Create a Position node set to Object space. This returns a Vector3 of our vertex position that we can then manipulate. For offsetting/displacing, we can use Add or Subtract nodes. But we can also scale the position, which pulls or pushes it from the origin (0,0,0), by using Multiply or Divide nodes.

Scaling should usually be done first, assuming you want to keep the offset in terms of object space units rather than the scaled space. We can scale/offset each vertex by connecting a Vector3 node and set each component separately, or use a Vector3 property to control it from the inspector, or a C# Script (via materialReference.SetVector(“_Ref”, vector), where _Ref is the reference string of the property in the shadergraph blackboard).

You can also Split and offset/scale each component separately then recombine in a Combine or Vector3 node, however this very quickly causes the graph to get messy with overlapping wires so I suggest using the Vector3 node/property approach instead.

The default values for these properties (so the position isn’t changed) would be : Scale (1,1,1) and Offset (0,0,0).

The graph above is basically the same as what the Tiling And Offset node does, but that only works with 2D (Vector2) coordinates (typically UV, for sampling textures). In this case our coordinates are 3D (Vector3) so we need to use Multiply & Add.

Below is another example if you wanted to scale both the X and Z with the same Vector1 property. Since we use a Multiply to adjust scale, we set the Y value to 1 so there is no change. (With offsetting we would use a value of 0 for no change)

We can also use a Time node to animate the offset over Time (or Sine Time, etc).

There will be more examples later in the post including a swaying effect for grass/plants and animating fish or butterflies.

Recalculating Normals

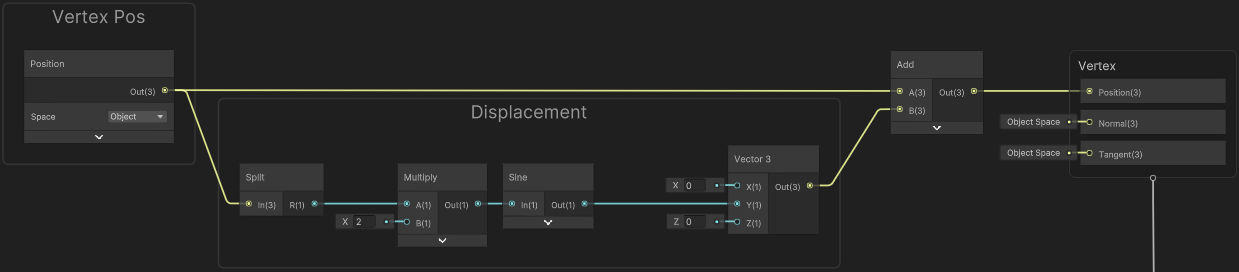
Consider this example displacement using a Sine wave :

On a highly subdivided plane mesh, this produces a result of :

This is using a Lit Graph, but the shading is the same as if this was a flat plane. This is because while we’ve edited the vertex positions, the normals remain unchanged. Here’s a few ways this could be fixed :

Per-Fragment

These methods are used in the Fragment stage, so connect to the Normal (Tangent space) or Normal (World space) ports. Which port is shown depends on the Fragment Normal Space defined in the Graph Settings. If you don’t need to support normal maps, it will be more performant to use World space.

Flat Normals

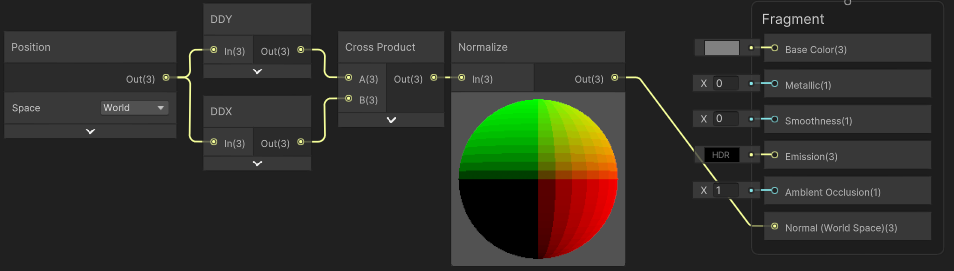
When used in the fragment stage, the Position node contains the displaced position. A simple way to obtain flat normals is by taking derivatives of this displaced vertices. This can be done with the DDY, DDX nodes and a Cross Product, then Normalize.

This results in :

Normal From Height

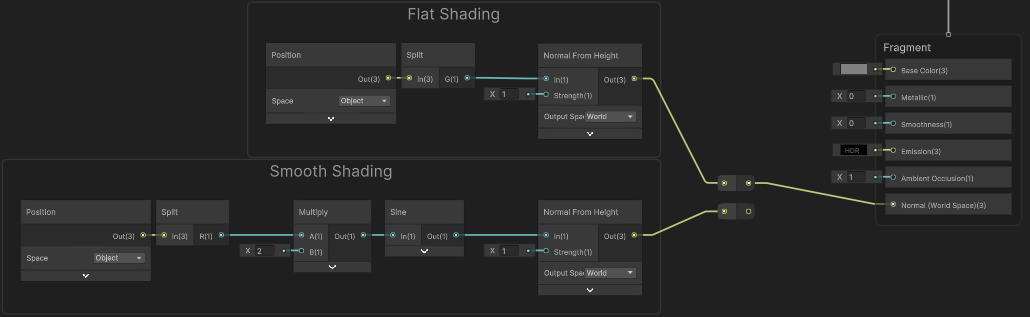
Another method to get normals is to use the Normal From Height node, which works well for flat planes like in our example. You’d want the output space to match the space used by the Fragment Normal Space defined in Graph Settings.

We could Split the Position and use the G output as our height (In input). But this again will result in a flat shading.

If you want a smooth shading, you’d instead need to replicate the displacement code in the fragment stage to calculate the height value. If the displacement is based on the original vertex positions you may want to pass those through a Custom Interpolator. In the case of our example, the X/R axis is used to calculate the displacement value, but only the Y/G axis is actually displaced, so we can actually still use the Position node.

The Normal From Height node also uses the screenspace derivative functions (ddx() and ddy()) to calculate differences between the positions at neighbouring pixels. It’s possible to do this as fragment shaders run in 2x2 pixel blocks. These methods are cheap in terms of performance, but as the same vector is calculated in that 2x2 pixel block it can look somewhat pixellated. (In the case of this Sine wave example I wouldn’t say this is noticeable though)

If you’re interested exactly how the node is implemented you can look at the generated code on the Node Library - Normal From Height page.

Normal From Texture

If you’re using a heightmap texture, there’s also the Normal From Texture node which can construct a normal map, which would be connected to the Normal (Tangent space) port in the Master Stack. This node uses multiple samples to calculate the normal vector.

If you’re interested exactly how the node is implemented you can look at the generated code on the Node Library - Normal From Texture page.

Per-Vertex

An alternative method to calculate normal vectors on a per-vertex basis, involves simulating neighbouring positions & displacements, taking their differences and using a cross product. But this only really works if the position is an input to the displacement calculation like it is in our example. This also means we need to do 3x the amount of displacement calculations, so could be more expensive.

In this case it’s easiest to use the Tangent Vector and Bitangent Vector to simulate these neighbours. The “Displacement” part of the graph here could be swapped out for other methods of displacement. This is based off this Wobble Displacement tutorial by Ronja.

Since the Displacement part of the graph needs to happen 3 times, it may be easier to put it in a SubGraph (with Vector3 input & output).

Returning to our scene/mesh, this results in smooth normals :

Bounds

Shaders run on the GPU, so it’s important to understand that it will not actually update the CPU-side mesh/vertices, mesh bounds or affect colliders.

If the camera goes outside the original bounds, the mesh renderer will be culled due to Frustum Culling - this is an optimisation Unity uses to avoid rendering objects outside of the camera view. But this can be a problem if our displaced vertices are outisde of these bounds. We either need to keep scaling/offsetting small, or override the bounds.

In 2021.2+ it’s now possible to override the Renderer.bounds (which is in world space) or Renderer.localBounds (which is local/object space, so the position/rotation/scale of the Transform component still applies). e.g.

1
2
3
4
5
6
7
8
9

Renderer renderer = GetComponent<Renderer>();
renderer.bounds = new Bounds(origin, size);
//or
renderer.localBounds = new Bounds(origin, size);

// And if you need to clear these bounds back to the default values, use :
renderer.ResetBounds();
// or
renderer.ResetLocalBounds();

In earlier versions, you’d need to override the Mesh.bounds itself. e.g.

1
2

Mesh mesh = GetComponent<MeshFilter>().mesh;
mesh.bounds = new Bounds(origin, size);

Note that this creates a new mesh instance, see MeshFilter.mesh. You are responsible for cleanup, so be sure to Destroy(mesh) in the MonoBehaviour.OnDestroy function! You’d usually use .sharedMesh instead if you don’t want to create a mesh instance. However then all objects that use that mesh will share those bounds, (and I’m unsure if you can even edit the bounds of a mesh from an imported model?)

As a tip for knowing what origin/size to use, add a Box Collider to the object, resize it, and use the center/size values, or GetComponent<BoxCollider>().bounds.

If you’re interested in updating colliders, maybe consider moving the vertex displacement to the CPU. See the Mesh class, mesh.vertices or mesh.GetVertices / SetVertices.

Uses

Some uses of vertex displacement:

• Adding detail to a mesh using displacement textures along with tessellation (which can’t be done in shadergraph yet as far as I know, at least not in URP).
• Animating vertices on a water plane to simulate waves. (See this catlikecoding tutorial for a good example)
• Creating various effects such as melting and wobbling. (I’ve done a melting candle effect, only shared on twitter though)
• Simulating wind on grass, plants and trees, see example below.
• Adding simple animation to regular meshes, instead of using skinned meshes. See below for examples of the motion of swimming fish and flapping butterfly/bird wings, which are fairly simple to simulate. The game ABZÛ also uses this a lot, see this ABZÛ GDC Talk.
• It’s also possible to bake actual skinned mesh animations to textures, and use the Vertex ID (SV_VertexID) to read the texture. While I haven’t used it, I am aware of this Mecanim2Texture tool by ryanslikesocool. I believe it also allows for baking Vertex IDs into a UV channel (as shader graph can’t use SV_VertexID yet), and some custom nodes for playback of the animations.

Examples

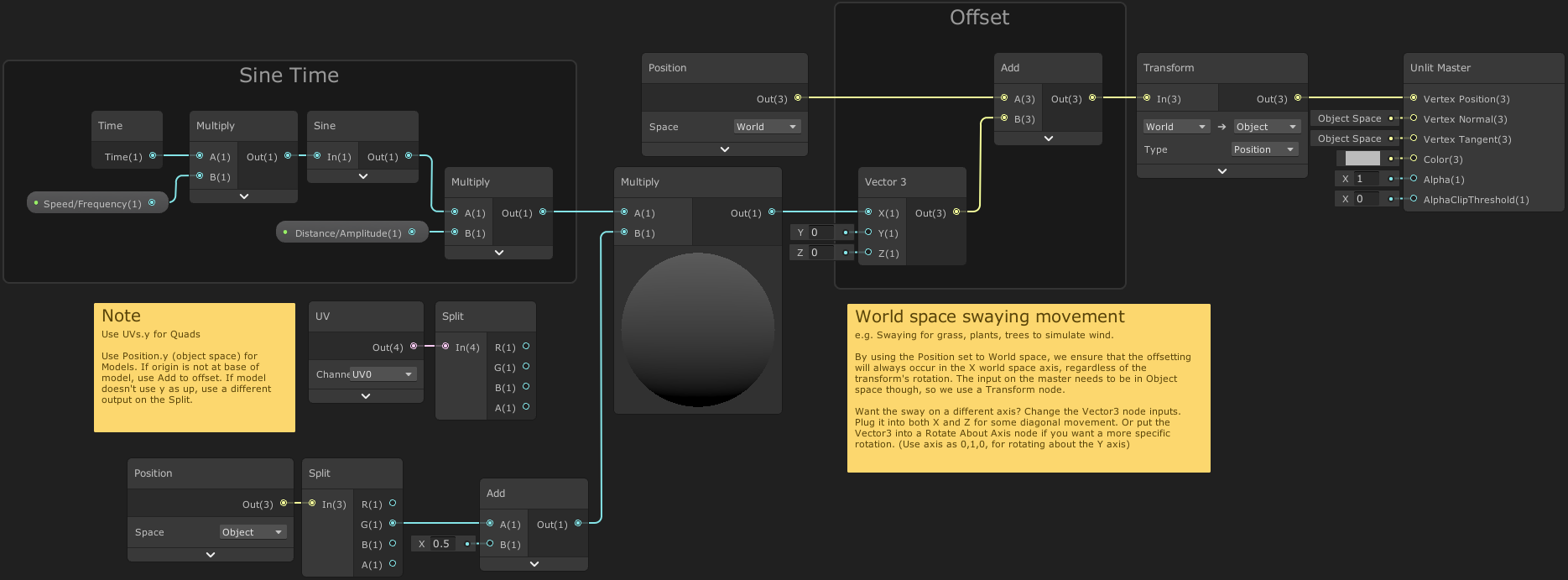
Swaying Grass

Right Note :

• By using the Position set to World space, we ensure that the offsetting will always occur in the X world space axis, regardless of the transform’s rotation. The input on the master needs to be in Object space though, so we use a Transform node.
• Want the sway on a different axis? Change the Vector3 node inputs. Plug it into both X and Z for some diagonal movement. Or put the Vector3 into a Rotate About Axis node if you want a more specific rotation. (Use axis as 0,1,0, for rotating about the Y axis)

Left Note :

• Use UVs.y for Quads. Use Position.y (object space) for Models. If origin is not at base of model, use Add to offset. If model doesn’t use y as up, use a different output on the Split.

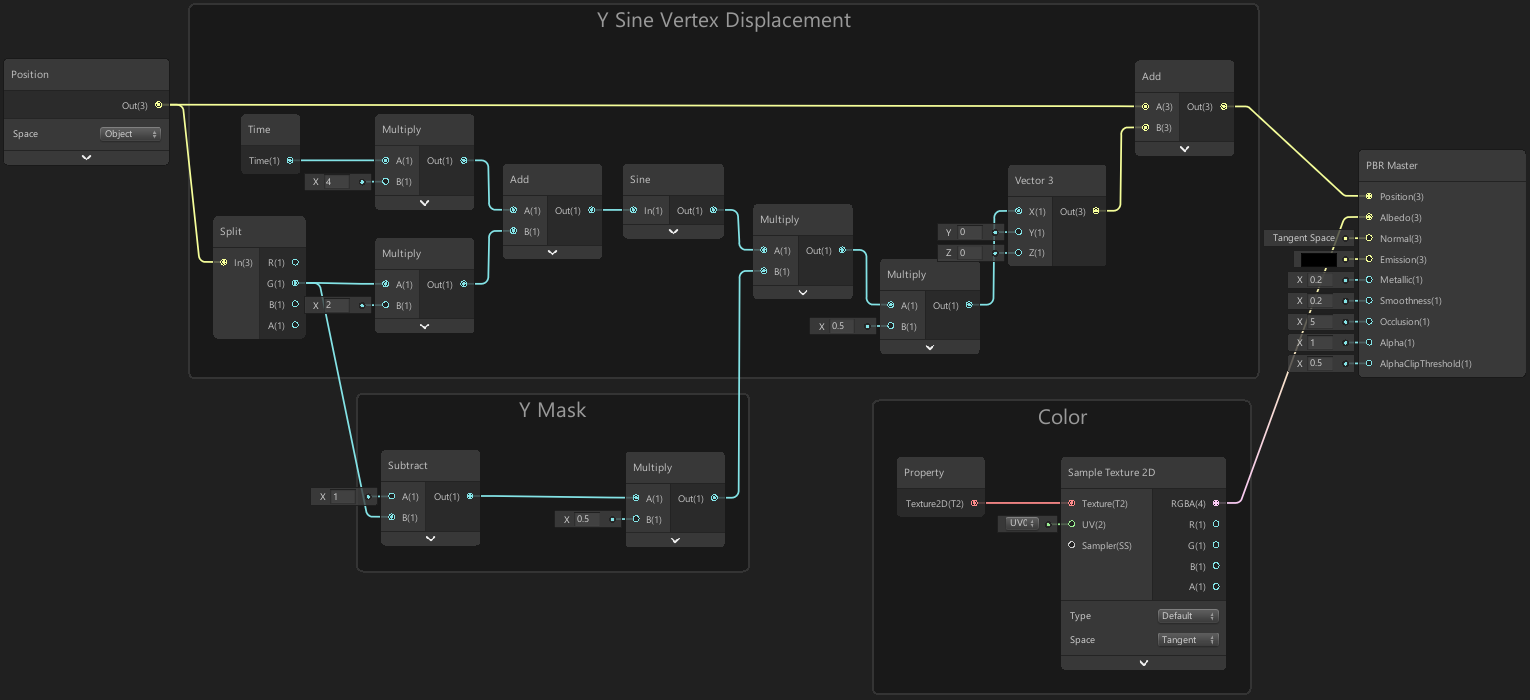
Swimming Motion (Fish)

A simple way to create a swimming motion for a fish, is to offset the R/X Position of the fish (left/right) by a Sine wave based on Time added with the position along the fish (forward/back, which is actually G/Y for the model I’m using). This can then be multiplied with a mask created from the G/Y position so vertices at the front of the fish move less.

In terms of code, this would be something along the lines of :

1

vertex.x += sin(vertex.y * 2 + _Time.y * 4) * (vertex.y - 1) * 0.25;

Note that values may vary based on the scale of the fish mesh. This was based on a model with 2 units length, with the origin being in the center.

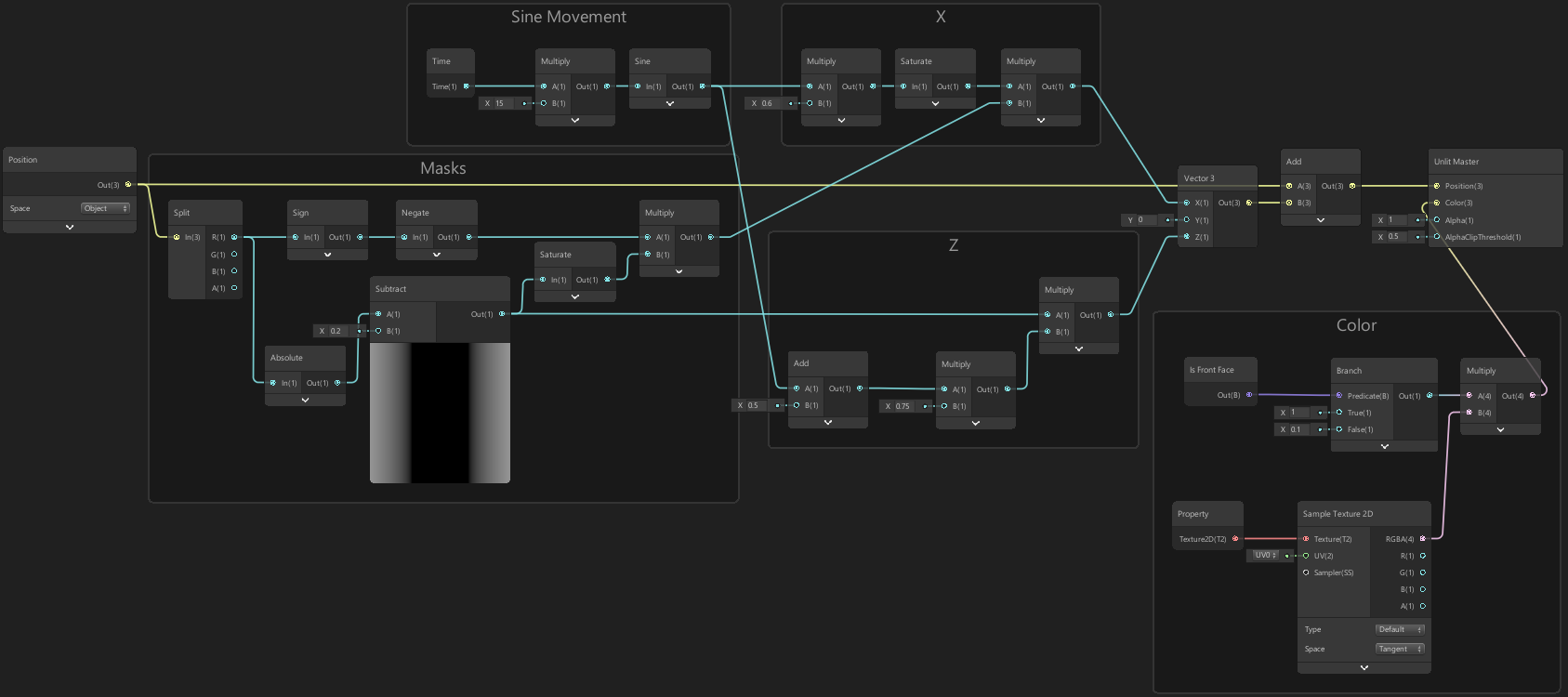
Wings Motion (Butterfly, or Bird)

For the motion of wings for a butterfly (see tweet in fish example above), we first create a mask based on the R/X (left/right) axis of the Position to determine how we offset the wings, which uses an Absolute so that we offset both wings in the same B/Z direction (which is up/down for this model).

We can then offset the B/Z position by a Sine wave based just on Time which will make the wings move linearly. If we want the wings to bend (which would be better for a bird) we can Add the mask to the Time output and put this into the Sine node instead.

We can also offset the R/X (left/right) a little, so as the wings go upwards they also move slightly inwards, which will reduce stretching and make the motion feel more realistic.

In terms of code, this would be something along the lines of :

1
2
3
4
5

float mask = abs(vertex.x) - 0.2;
float s = sin(_Time.y * 15.0); // for butterfly
// or : float s = sin(_Time.y * 10.0 + mask) // for bird
vertex.x += saturate(s * 0.6) * saturate(mask) * -1.0 * sign(vertex.x);
vertex.z += (s + 0.5) * 0.75 * mask;

Note that values may vary based on the scale of the butterfly mesh. This was based on a model of 2 by 2 units, with the origin being in the center.

Other

The following tutorial breakdowns that I’ve written also include vertex displacement :

• Whirlpool
• Jellyfish
• Cloud
• Foliage
• Tornado
• Tentacle

Join my discord! 💬